Whisker plots of parameter posterior distributions

Displays whisker plots for specified parameters on the same plot, with a point at the mean value for the posterior distribution and whiskers extending to the specified quantiles of the distribution.

whiskerplot(x, parameters, quantiles=c(0.025,0.975), zeroline=TRUE, ...)

Arguments

x

A jagsUI object

parameters

A vector of names (as characters) of parameters to include in the plot. Parameter names must match parameters included in the model. Calling non-scalar parameters without subsetting (e.g. alpha) will plot all values of alpha.

quantiles

A vector with two values specifying the quantile values (lower and upper).

zeroline

If TRUE, a horizontal line at zero is drawn on the plot.

...

Additional arguments passed to plot.default

Author

Ken Kellner contact@kenkellner.com.

Examples

#Analyze Longley economic data in JAGS
#Number employed as a function of GNP
#See ?jags for a more detailed example

#Get data
data(longley)
gnp <- longley$GNP
employed <- longley$Employed
n <- length(employed)
data <- list(gnp=gnp,employed=employed,n=n)

#Identify filepath of model file
modfile <- tempfile()

writeLines("
model{

  #Likelihood
  for (i in 1:n){ 

    employed[i] ~ dnorm(mu[i], tau)     
    mu[i] <- alpha + beta*gnp[i]

  }
    
  #Priors
  alpha ~ dnorm(0, 0.00001)
  beta ~ dnorm(0, 0.00001)
  sigma ~ dunif(0,1000)
  tau <- pow(sigma,-2)

}
", con=modfile)

#Set parameters to monitor
params <- c('alpha','beta','sigma','mu')

#Run analysis

out <- jags(data = data,
            inits = NULL,
            parameters.to.save = params,
            model.file = modfile,
            n.chains = 3,
            n.adapt = 100,
            n.iter = 1000,
            n.burnin = 500,
            n.thin = 2)
#> 
#> Processing function input....... 
#> 
#> Done. 
#>  
#> Compiling model graph
#>    Resolving undeclared variables
#>    Allocating nodes
#> Graph information:
#>    Observed stochastic nodes: 16
#>    Unobserved stochastic nodes: 3
#>    Total graph size: 74
#> 
#> Initializing model
#> 
#> Adaptive phase, 100 iterations x 3 chains 
#> If no progress bar appears JAGS has decided not to adapt 
#>  
#> 
#>  Burn-in phase, 500 iterations x 3 chains 
#>  
#> 
#> Sampling from joint posterior, 500 iterations x 3 chains 
#>  
#> 
#> Calculating statistics....... 
#> 
#> Done. 

#Examine output summary

out
#> JAGS output for model '/tmp/RtmpWkPEqM/fileaa566bbbd634', generated by jagsUI.
#> Estimates based on 3 chains of 1000 iterations,
#> adaptation = 100 iterations (sufficient),
#> burn-in = 500 iterations and thin rate = 2,
#> yielding 750 total samples from the joint posterior. 
#> MCMC ran for 0 minutes at time 2026-01-29 15:20:57.627967.
#> 
#>            mean    sd   2.5%    50%  97.5% overlap0 f  Rhat n.eff
#> alpha    51.841 0.753 50.399 51.825 53.254    FALSE 1 1.000   750
#> beta      0.035 0.002  0.031  0.035  0.039    FALSE 1 1.001   750
#> sigma     0.718 0.147  0.499  0.697  1.040    FALSE 1 0.999   750
#> mu[1]    59.985 0.333 59.336 59.976 60.645    FALSE 1 1.000   750
#> mu[2]    60.859 0.293 60.279 60.849 61.441    FALSE 1 1.000   750
#> mu[3]    60.812 0.295 60.227 60.801 61.396    FALSE 1 1.000   750
#> mu[4]    61.734 0.255 61.233 61.727 62.253    FALSE 1 1.000   750
#> mu[5]    63.277 0.201 62.885 63.275 63.696    FALSE 1 1.001   750
#> mu[6]    63.903 0.185 63.539 63.910 64.284    FALSE 1 1.001   750
#> mu[7]    64.542 0.175 64.206 64.546 64.882    FALSE 1 1.002   750
#> mu[8]    64.463 0.176 64.123 64.467 64.812    FALSE 1 1.001   750
#> mu[9]    65.658 0.174 65.324 65.660 66.013    FALSE 1 1.002   716
#> mu[10]   66.412 0.185 66.043 66.411 66.776    FALSE 1 1.003   693
#> mu[11]   67.232 0.207 66.854 67.229 67.643    FALSE 1 1.004   699
#> mu[12]   67.294 0.208 66.912 67.293 67.714    FALSE 1 1.004   700
#> mu[13]   68.621 0.257 68.086 68.626 69.162    FALSE 1 1.004   740
#> mu[14]   69.312 0.286 68.710 69.313 69.922    FALSE 1 1.004   750
#> mu[15]   69.854 0.311 69.213 69.856 70.511    FALSE 1 1.003   750
#> mu[16]   71.130 0.371 70.382 71.136 71.932    FALSE 1 1.003   750
#> deviance 33.138 2.788 30.069 32.472 40.458    FALSE 1 1.002   750
#> 
#> Successful convergence based on Rhat values (all < 1.1). 
#> Rhat is the potential scale reduction factor (at convergence, Rhat=1). 
#> For each parameter, n.eff is a crude measure of effective sample size. 
#> 
#> overlap0 checks if 0 falls in the parameter's 95% credible interval.
#> f is the proportion of the posterior with the same sign as the mean;
#> i.e., our confidence that the parameter is positive or negative.
#> 
#> DIC info: (pD = var(deviance)/2) 
#> pD = 3.9 and DIC = 37.032 
#> DIC is an estimate of expected predictive error (lower is better).

#Generate whisker plots

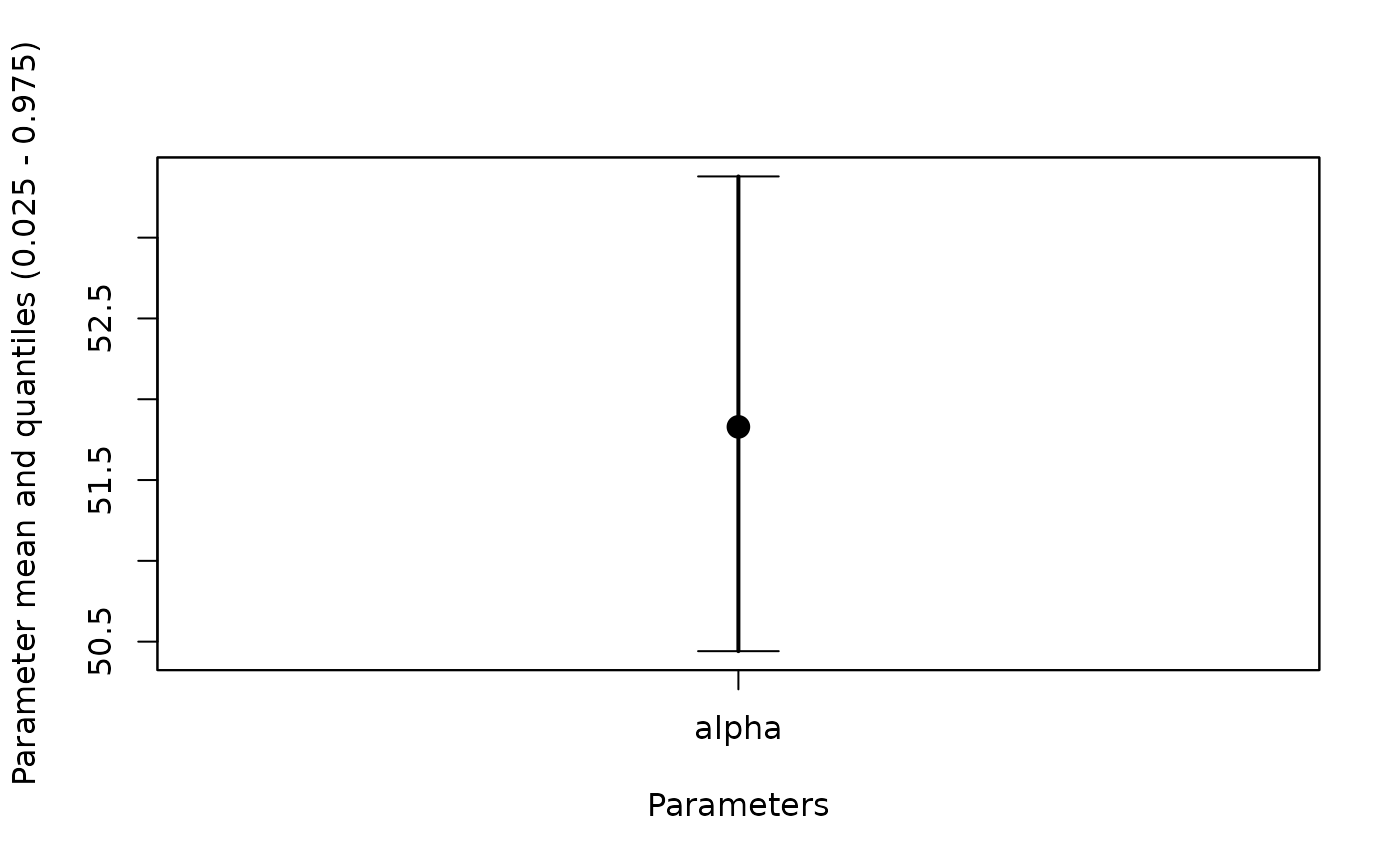
#Plot alpha

whiskerplot(out,parameters=c('alpha'))


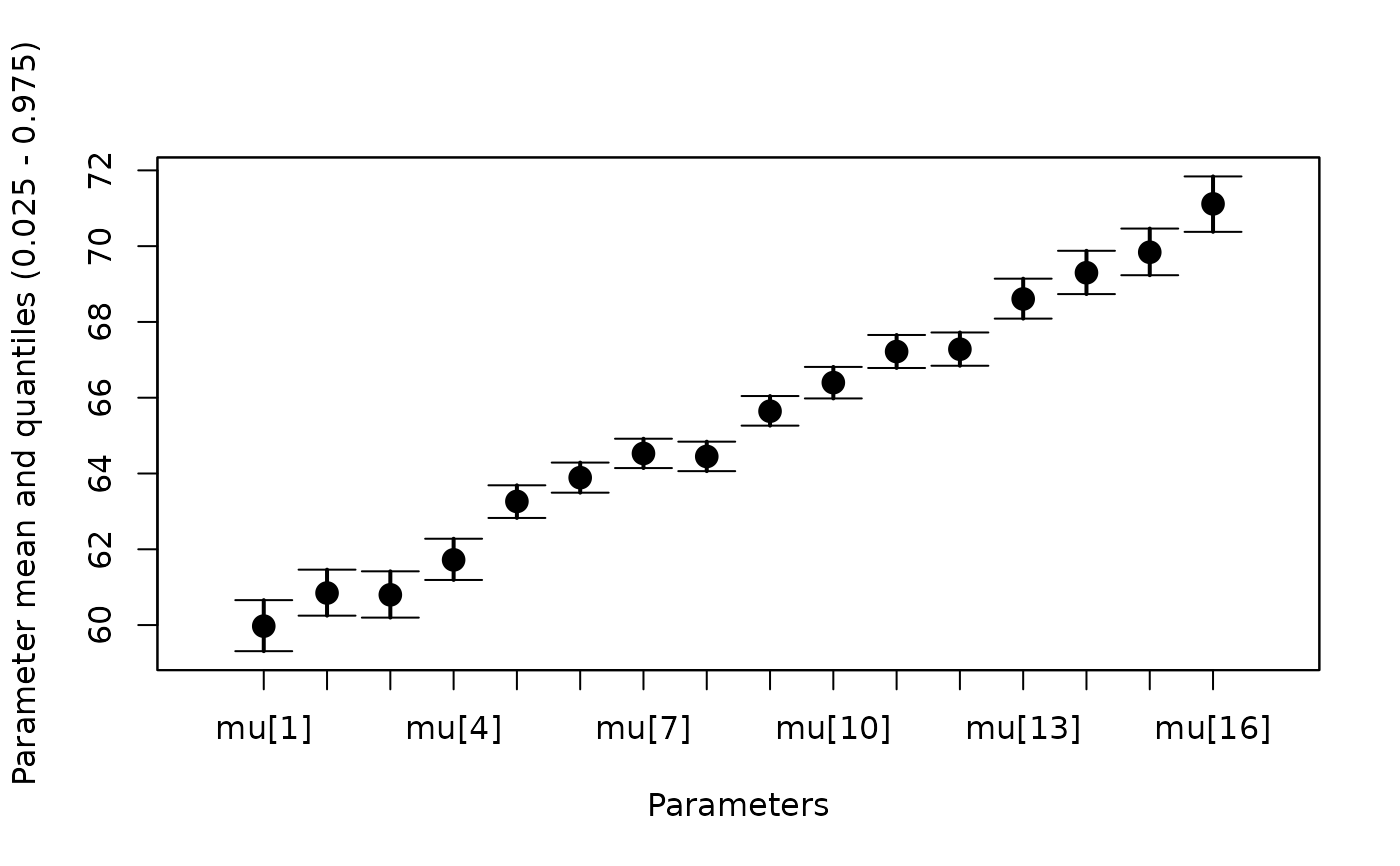
#Plot all values of mu

whiskerplot(out,parameters='mu')


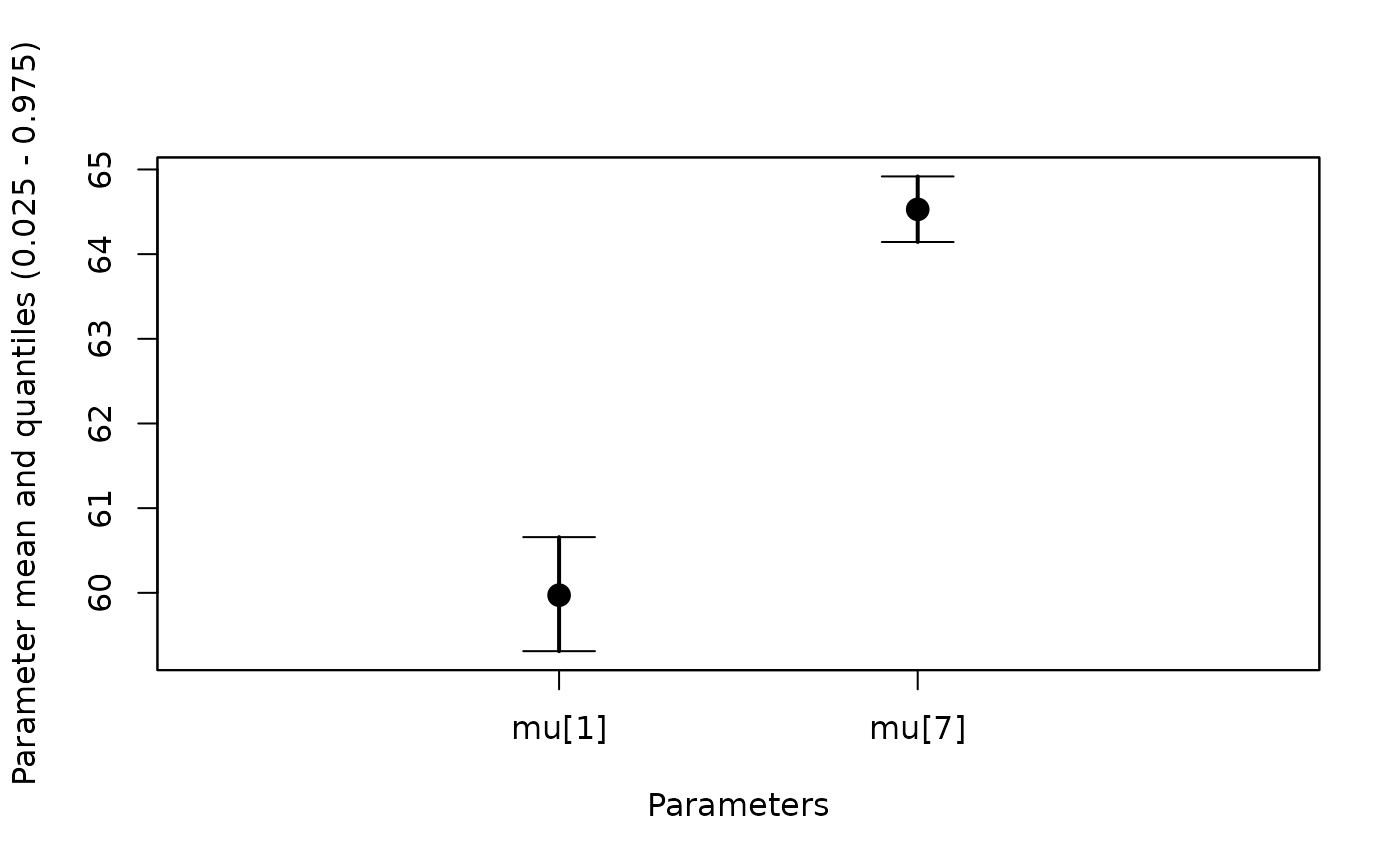
#Plot a subset of mu

whiskerplot(out,parameters=c('mu[1]','mu[7]'))


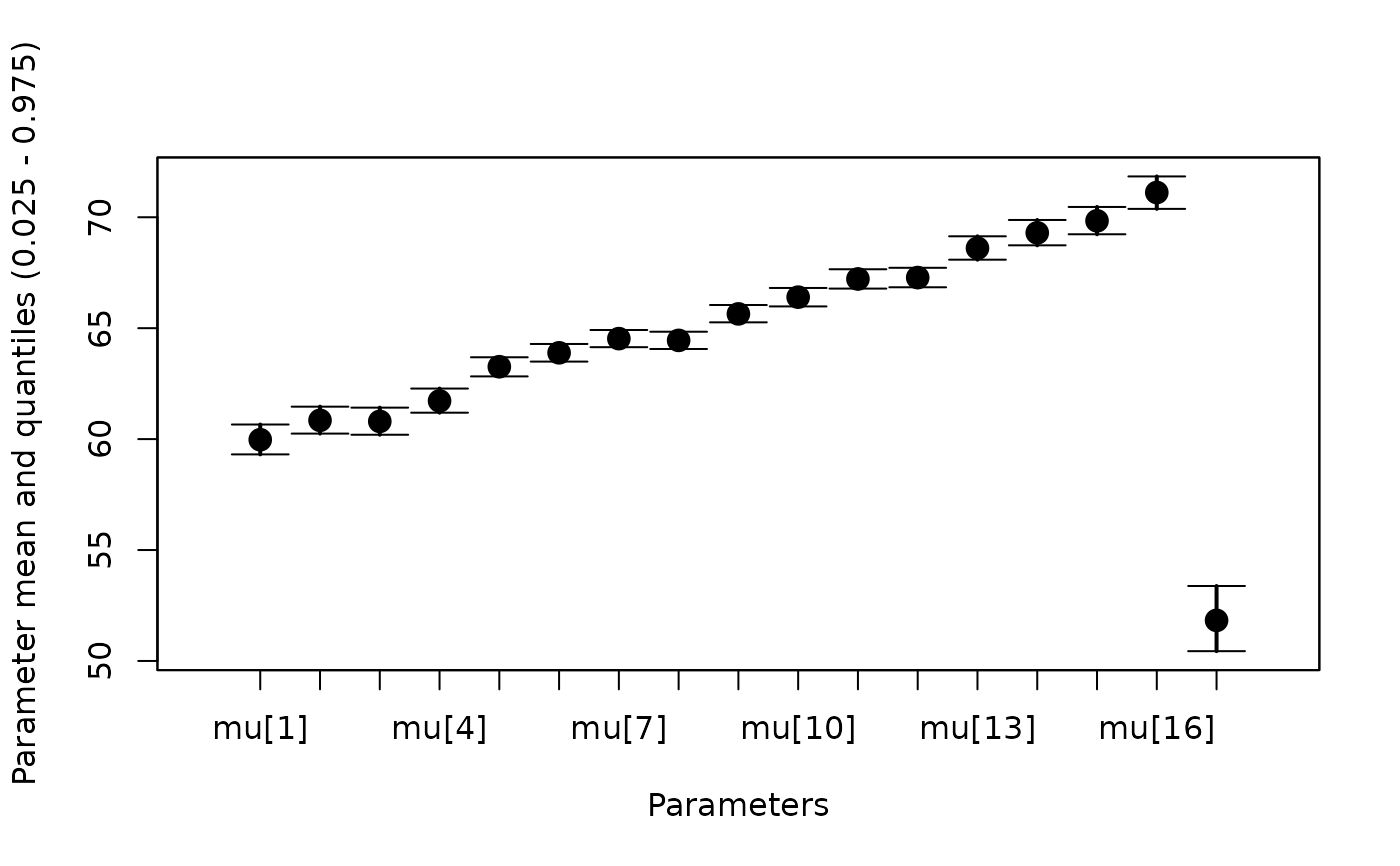
#Plot mu and alpha together

whiskerplot(out,parameters=c('mu','alpha'))