Posterior Predictive Checks for Bayesian Analyses fit in JAGS

A simple interface for generating a posterior predictive check plot for a JAGS analysis fit using jagsUI, based on the posterior distributions of discrepency metrics specified by the user and calculated and returned by JAGS (for example, sums of residuals). The user supplies the name of the discrepancy metric calculated for the real data in the argument observed, and the corresponding discrepancy for data simulated by the model in argument simulated. The posterior distributions of the two parameters will be plotted in X-Y space and a Bayesian p-value calculated.

pp.check(x, observed, simulated, xlab='Observed data', ylab='Simulated data', 
                     main='Posterior Predictive Check', ...)

Arguments

x

A jagsUI object generated using the jags function

observed

The name of the parameter (as a string) representing the fit of the observed data (e.g. residuals)

simulated

The name of the corresponding parameter (as a string) representing the fit of the new simulated data

xlab

Customize x-axis label

ylab

Customize y-axis label

main

Customize plot title

...

Additional arguments passed to plot.default

Author

Ken Kellner contact@kenkellner.com.

Examples

#Analyze Longley economic data in JAGS
#Number employed as a function of GNP
#See ?jags for a more detailed example

#Get data
data(longley)
gnp <- longley$GNP
employed <- longley$Employed
n <- length(employed)
data <- list(gnp=gnp,employed=employed,n=n)

#Identify filepath of model file
modfile <- tempfile()

#Write model
#Note calculation of discrepancy stats fit and fit.new
#(sums of residuals)
writeLines("
model{

  #Likelihood
  for (i in 1:n){ 

    employed[i] ~ dnorm(mu[i], tau)     
    mu[i] <- alpha + beta*gnp[i]
    
    res[i] <- employed[i] - mu[i]   
    emp.new[i] ~ dnorm(mu[i], tau)
    res.new[i] <- emp.new[i] - mu[i]

  }
    
  #Priors
  alpha ~ dnorm(0, 0.00001)
  beta ~ dnorm(0, 0.00001)
  sigma ~ dunif(0,1000)
  tau <- pow(sigma,-2)
  
  #Derived parameters
  fit <- sum(res[])
  fit.new <- sum(res.new[])

}
", con=modfile)

#Set parameters to monitor
params <- c('alpha','beta','sigma','fit','fit.new')

#Run analysis

out <- jags(data = data,
            inits = NULL,
            parameters.to.save = params,
            model.file = modfile,
            n.chains = 3,
            n.adapt = 100,
            n.iter = 1000,
            n.burnin = 500,
            n.thin = 2)
#> 
#> Processing function input....... 
#> 
#> Done. 
#>  
#> Compiling model graph
#>    Resolving undeclared variables
#>    Allocating nodes
#> Graph information:
#>    Observed stochastic nodes: 16
#>    Unobserved stochastic nodes: 19
#>    Total graph size: 126
#> 
#> Initializing model
#> 
#> Adaptive phase, 100 iterations x 3 chains 
#> If no progress bar appears JAGS has decided not to adapt 
#>  
#> 
#>  Burn-in phase, 500 iterations x 3 chains 
#>  
#> 
#> Sampling from joint posterior, 500 iterations x 3 chains 
#>  
#> 
#> Calculating statistics....... 
#> 
#> Done. 

#Examine output summary

out
#> JAGS output for model '/tmp/RtmpWkPEqM/fileaa5643eba4c', generated by jagsUI.
#> Estimates based on 3 chains of 1000 iterations,
#> adaptation = 100 iterations (sufficient),
#> burn-in = 500 iterations and thin rate = 2,
#> yielding 750 total samples from the joint posterior. 
#> MCMC ran for 0 minutes at time 2026-01-29 15:20:57.214734.
#> 
#>            mean    sd   2.5%    50%  97.5% overlap0     f  Rhat n.eff
#> alpha    51.825 0.737 50.315 51.835 53.335    FALSE 1.000 1.000   750
#> beta      0.035 0.002  0.031  0.035  0.038    FALSE 1.000 1.001   750
#> sigma     0.720 0.158  0.488  0.692  1.076    FALSE 1.000 1.005   750
#> fit      -0.020 2.932 -5.756 -0.006  5.922     TRUE 0.501 0.999   750
#> fit.new   0.039 2.871 -5.191 -0.077  6.042     TRUE 0.483 1.006   369
#> deviance 33.338 2.941 30.012 32.466 40.361    FALSE 1.000 1.002   750
#> 
#> Successful convergence based on Rhat values (all < 1.1). 
#> Rhat is the potential scale reduction factor (at convergence, Rhat=1). 
#> For each parameter, n.eff is a crude measure of effective sample size. 
#> 
#> overlap0 checks if 0 falls in the parameter's 95% credible interval.
#> f is the proportion of the posterior with the same sign as the mean;
#> i.e., our confidence that the parameter is positive or negative.
#> 
#> DIC info: (pD = var(deviance)/2) 
#> pD = 4.3 and DIC = 37.664 
#> DIC is an estimate of expected predictive error (lower is better).

#Posterior predictive check plot

pp.check(out, observed = 'fit', simulated = 'fit.new')

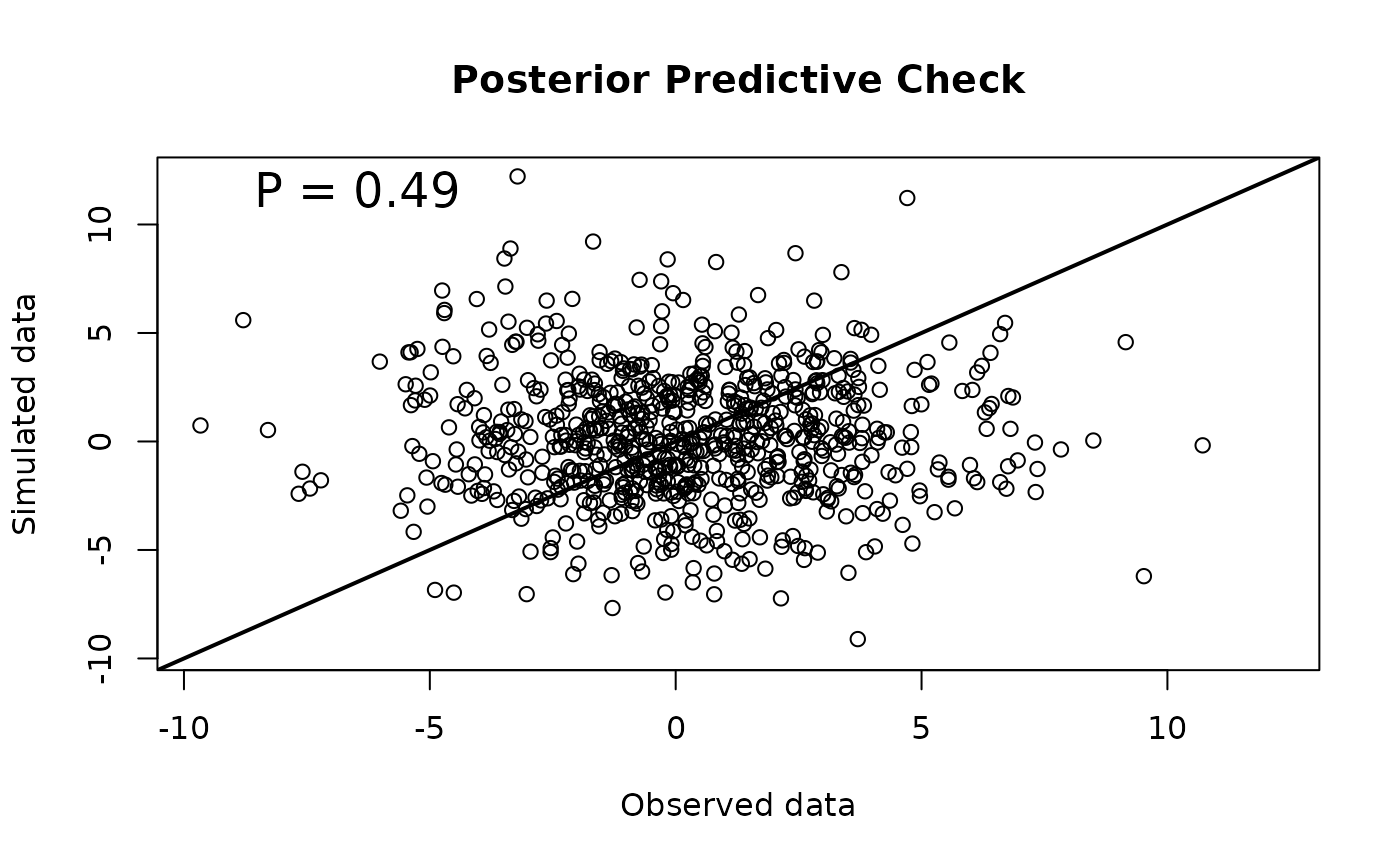#> [1] 0.4946667